APCS Problem Set 4a: Algorithms and Basic Flow Control

Michael Ferraro
mferraro@balstaff.org
Balboa High School
22 September 2015

Contents

• 1 Introduction
  • 1.1 Objectives
  • 1.2 Due Date
  
  
• 2 Getting Started with Algorithms
  • 2.1 Required Reading
  • 2.2 Basic Ideas
  
  
• 3 Iteration
  • 3.1 Required Reading
  • 3.2 Loops in Java
  • 3.3 Iterative Addition
  • 3.4 Iteration Exercises
  • 3.5 Iteration Book Problems
  
  
• 4 Euclid's GCF Algorithm (Litvin §7.7)

1 Introduction

As you are learning in class, an algorithm is a description of a step-by-step process to achieve some desired result. For instance, if you wanted to calculate 8283 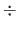$\div$ 7 by hand, you would follow the long division algorithm that you were taught in grade school.

Inherent in many algorithms are loops, where steps may be repeated under different conditions. Long division ``loops'' when you perform this set of steps repeatedly: Write a digit on top of the division bracket, multiply that digit by the divisor, writing the result below the dividend's digit(s) into which you are currently dividing, subtract, and bring down the next digit of the dividend to join the result of the subtraction. But then there's a stopping condition: If there are no more digits to bring down from the dividend, you use the remaining amount as the numerator of a fraction representing the remainder.

Perhaps you found that process description difficult to follow. You will learn that flowcharts are sometimes used to visually represent a process. And then there's pseudocode, which allows you to describe how a process works in a written form that is more compact and faster to write than full-on Java code.

There are often multiple algorithms that can carry out a specific task. Some have advantages over others: Running in fewer steps, requiring less memory, or simply being easier to write (implement) in a high-level programming language.

University CS programs often have entire courses dedicated to the study of algorithms. Such courses are typically considered to be studies in Computer Science and Discrete Mathematics.

1.1 Objectives

By completing this problem set, students will learn to...

• write simple algorithms in Java,
• analyze the operation of prewritten algorithms,
• differentiate between iterative and recursive procedures,
• work with elements of a list using the Java for-each facility, and
• use while statements to affect the flow of a program.

1.2 Due Date

This problem set is tentatively due before 5th Period on 5 October 2015.

2 Getting Started with Algorithms

2.1 Required Reading

$\rightarrow$ Litvin & Litvin, Java Methods A & AB: §§7.1-7.2

2.2 Basic Ideas

1. Based on the reading, what is it called when an algorithm has a set of instructions that may be repeated multiple times? (1-to-2 word answer expected!)
   #INPUT:repeating-set-of-instructions#
2. From what you read about pseudocode, explain what this expression means: b $\leftarrow$ 9.
   #INPUT:explain-value-assignment#
3. Summarize Litvin's rules for flowcharts:
   
   
   • Rectangles represent #INPUT:rectangles#
     
   • Parallelograms represent #INPUT:parallelograms#
     
   • Diamonds represent #INPUT:diamonds#
     

3 Iteration

3.1 Required Reading

$\rightarrow$ Litvin & Litvin, Java Methods A & AB: §7.3 -- only read pp184-186.

3.2 Loops in Java

1. What are the two kinds of loops Litvin mentions that support iteration in Java?
   #INPUT:two-kinds-of-loops#
2. What are the three elements that a loop must have? Number them: (1) ... (2) ... (3) ...
   #INPUT:three-elts-loop#

3.3 Iterative Addition

Consider this pseudocode, which describes a way to find the sum of a list of integers iteratively:


Input: LIST, a list of integers to be added together

sum 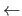$\leftarrow$ 0

While there are still elements in LIST:
    sum 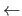$\leftarrow$ sum + (first element in LIST)
    remove first element of LIST

Output: sum


If we were to run the iterative procedure with this set of integers -- {52, 118, 917, 36, 661, 98} -- the variable state just before the first iteration of the while loop would be:

sum = 0
LIST = ( 52, 118, 917, 36, 661, 98 )

After the while loop runs once, here is the variable state:

sum = 52
LIST = ( 118, 917, 36, 661, 98 )

The value of LIST's first element, 52, was added to sum, and that element was removed from LIST -- leaving 118 to be the new first element.

Now that you've seen a pseudocode version of this addition algorithm, examine an interactive version, written in Scratch:

1. Download IterativeAddition.sb2 from http://feromax.com/apcs/problemsets/PS04a/downloads/IterativeAddition/.
   
   
2. Start Scratch in your web browser by visiting https://scratch.mit.edu/projects/editor/ in a new window/tab.
   
   
3. Within Scratch, go to File $\rightarrow$ Upload from your computer, and select the file you downloaded, IterativeAddition.sb2.
   
   
4. Click the green flag to begin.

In the table (see paper form), show the variable state after each iteration until the stopping condition is reached (i.e., there are no more values in LIST). Then, list the total number of iterations to the right. Note: When counting the total number of iterations, don't count the 0$^{th}$ one. #INPUT:interative-addition-table#

3.4 Iteration Exercises

Write Java code that could be placed inside a class' main() to...

1. Print all elements in the set $\{ -100, -99, -98, \ldots , -3, -2, -1 \}$.
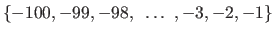   #INPUT:print-elts-neg100_through_neg1#
2. Print every multiple of 3 from 0 to 72, inclusive.
   #INPUT:print-elts-0_to_72-by-3s#

3.5 Iteration Book Problems

For these problems, it is best to write your solutions on scratch paper first before writing the final versions below.

1. Ch. 7, #16. Complete the table (see paper form), circling the return value. Iteration refers to the number of times the loop has been run.
   #INPUT:ch7_16#
   
   
2. Ch. 7, #5. Here is a hint for the $<$ missing code $>$ block:

       while ( n > 0 ) { 
           // ???
       }
   

   #INPUT:ch7_5#
   
   
3. Ch. 7, #1. On the paper form, you are provided with a partial flowchart to compute the sum. Fill in the 5 blanks and be sure to test your solution by tracing the variable values on a piece of paper. Hint: The first term in the series, 1, is actually $\frac{1}{1^2}$.
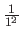   #INPUT:ch7_1#
   
   
4. Ch. 7, #4. In the same way one might think of multiplication as repeated addition operations, division may be thought of as repeated subtraction operations. Consult this Scratch example to help you: Upload DivisionExample.sb2 from http://feromax.com/apcs/problemsets/PS04a/downloads/DivisionExample/ to Scratch at https://scratch.mit.edu/projects/editor/.

   Import Ch7Num4.java from http://feromax.com/apcs/problemsets/PS04a/downloads/Ch7Num4-division/. Take note of how ints a and b are sent to the divide() method, which will then print the result of a 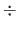$\div$ b (including the remainder). Your job is to supply the missing code in the divide() method and then write the statements you add to the paper form.
   #INPUT:ch7_4#
   
   

5. Ch. 7, #3.
   #INPUT:ch7_3#

4 Euclid's GCF Algorithm (Litvin §7.7)

1. Copy the flowchart for Euclid's GCF Algorithm from Livtin §7.7.
#INPUT:gcf-alg-diagram#

2. If the process described by the flowchart were part of a method called GCF(), and we made the method call shown below, how many iterations would it take to find the GCF¹? Show your scratch work on the paper form.

     int myGCF = GCF( 24, 36 );

#INPUT:myGCF-trace#

3. How many iterations would finding

     GCF( 40, 16 )

take? Show your scratch work on the paper form.
#INPUT:GCF_40-16#

Reaffirmation of Academic Honesty

Have you continued to follow the course's policy on academic honesty, as described in the syllabus and in Problem Set #1?
#INPUT:academic-honesty#

Footnotes

... GCF¹

Greatest Common Factor, i.e. the largest whole-number divisor of two or more whole numbers.