Litvin & Litvin, Java Methods A & AB: §§13.1
13.2
Consider this simple arithmetic expression:
int sum = 52 + 118 + 917 + 36 + 661 + 98;
In this case, Java runs its own arithmetic evaluator over the original arithmetic expression. What we will do here is develop a way to evaluate a sum using a recursive algorithm.
Recall that a recursive solution breaks a problem into simpler subproblems, each one resembling the original. You can think of the problem recursively in these terms:
Here is pseudocode describing the process:
Input: LIST, a list of integers to be added together
If LIST is empty:
return 0
sum 
(first element in LIST) + (result of running this algorithm on rest of LIST)
Output: sum
If we run this algorithm over our sum from earlier, you will notice below that the sum is effectively calculated from right to left -- opposite of our iterative approach from §3.3 of PS4a.
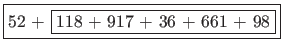
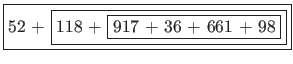
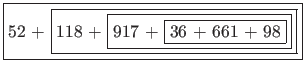
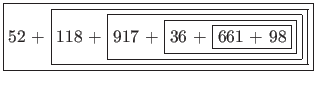
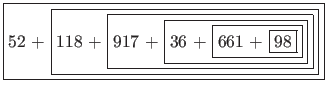
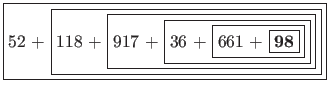
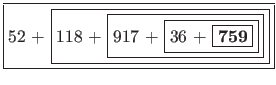
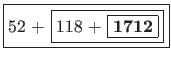
If our pseudocode were implemented in Java as a method called sumOf(), calling that method with our list of numbers from earlier would resemble
),
).
|
sumOf(
)
52 + sumOf(
52 + ( 118 + sumOf(
52 + ( 118 + ( 917 + sumOf(
52 + ( 118 + ( 917 + ( 36 + sumOf(
52 + ( 118 + ( 917 + ( 36 + ( 661 + sumOf( 52 + ( 118 + ( 917 + ( 36 + ( 661 + ( 98 + sumOf() ) ) ) ) ) 52 + ( 118 + ( 917 + ( 36 + ( 661 + ( 98 + 0 ) ) ) ) ) 52 + ( 118 + ( 917 + ( 36 + ( 661 + 98 ) ) ) ) 52 + ( 118 + ( 917 + ( 36 + 759 ) ) ) 52 + ( 118 + ( 917 + 795 ) ) 52 + ( 118 + 1712 ) 52 + 1830 1882
|
Notice the widest printed line above? That execution occurs just as this recursive procedure is using the most memory. In fact, that's a key weakness of recursive procedures: They tend to use more memory than their iterative counterparts.
The key features of a recursive procedure are
What would a Java implementation of the recursive algorithm look like? Consider this program:1
import java.util.ArrayList;
public class SumOfRec {
public static int sumOf(ArrayList<Integer> list) {
if ( list.isEmpty() ) { //base case
return 0;
}
//strip off first element
int firstElt = list.remove(0);
//recursive call to sumOf()
return firstElt + sumOf(list);
}
public static void main(String[] args) {
// create a list of integers to be added together
ArrayList<Integer> myList = new ArrayList<Integer>();
myList.add(52); //first element
myList.add(118);
myList.add(917);
myList.add(36);
myList.add(661);
myList.add(98); //last element
int sum = sumOf(myList);
System.out.print("The sum of the elements in " + myList
+ " is " + sum + ".");
}
}
Run the class. Once you verify that it's working, comment out the base case by putting the multi-line comment tags around it:
/*
if ( list.isEmpty() ) { //base case
return 0;
}
*/
) around the final result that would be returned.
Litvin & Litvin, Java Methods A & AB (1st Ed.): PDF version of §4.6 -- download from http://feromax.com/apcs/problemsets/PS04b/downloads/protected/
element, moving up toward the 599, before finding the number you set out to find?
All of the directories (folders) on a computer can be thought of as a tree with a root, branches, subbranches, sub-subbranches, etc. A directory may contain subdirectories and/or files. All directories have the special entries ``.'' and ``..'' except the root directory, which is missing the ``..'' entry. (Why do you think the root directory is missing ``..''?)
Consider this problem: You want to write a program that represents a filesystem consisting of directories and files. Once you've represented a directory tree in your program, how could you go about determining the entire number of files contained in a directory -- including the files contained in the subdirectories? (That directory could be the root directory, allowing you to find the total number of files in the entire filesystem.) A similar problem could be how to find the total space taken up by a directory and all its subdirectories.
Litvin & Litvin, Java Methods A & AB: §13.4 -- read the notes below to help you understand the reading.
Notes:
0
count + 1
count + fileCount(item)
If you look at the source for the Folder class, you'll notice this line:
private ArrayList<FilingItem> items = new ArrayList<FilingItem>();
Every folder will have a collection of items stored within it, a collection of FilingItems. These items might be Files or Folders, but they're all considered to be FilingItems. Hence, we will simply have an ArrayList populated with FilingItems.
Look at the fileCount() method from the Folder class:
public int fileCount() {
int count = 0;
for ( FilingItem curItem : items ) {
count = count + curItem.fileCount();
}
return count;
}
|
For example, if the object is a FilingItem, but more specifically a File, Java will see if there is a fileCount() method available for use in the File class. If not, Java uses the version of the method available in the FilingItem class. This feature is called polymorphism, which we will explore in greater detail later.
Try running the FileManager class. Then look through the class' main() to see what it's actually doing.
/home/student/Documents/ps1.doc
In order to do that, you'll need to create 1 additional folder, a file, and then make sure the file and folder are properly connected to each other and the existing file system provided to you.
Litvin & Litvin, Java Methods A & AB: §13.5
printStars(1);
printStars(2);
printStars(3);
printStars(4);
#INPUT:old_ch4_8a#
// Returns the product of a and b
// Precondition: a>=0, b>=0
public int product(int a, int b)
{
...
}
#INPUT:old_ch4_10#