APCS Problem Set 8: FactorQuadratics Team Assignment
You were taught the process of factoring a quadratic expression years ago. While the methods you were taught may have varied, they all boil down to some form of guess and check. Consider this quadratic expression, which happens to be a trinomial1: 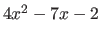 . When factoring into a product of binomials --
. When factoring into a product of binomials --
( __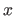 + __ )( __
+ __ )( __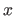 + __ )
+ __ )
-- the only possible integer coefficients of 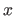 are the factors of 4 from
are the factors of 4 from 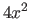 :
:  . And the only possible integer values for the constant in each binomial are the factors of -2:
. And the only possible integer values for the constant in each binomial are the factors of -2:
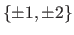 . Ordinarily, you'd have to try one or more combinations of values from each set and see whether the ``outer'' and ``inner'' pairs have a product equal to the original expression's middle term,
. Ordinarily, you'd have to try one or more combinations of values from each set and see whether the ``outer'' and ``inner'' pairs have a product equal to the original expression's middle term, 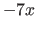 .
.
If you were taught a pure guess and check method, you were likely taught some specific ``moves'' you can make -- e.g., swapping the constants between the two binomials and inverting the constants' signs -- in order to find a correct factorization. These ideas were presented as ways to minimize the number of tries it would take before finding the correct answer. But what if you wanted a computer to perform the same function? Would you program each of your ``tricks''? Or would it be more time effective to write a program that can exhaustively search all possible combinations of coefficients and break out of a loop when the right combination is found?
By completing this problem set, students will learn to...
- use nested for() loops to have a program test all possible combinations of values for two or more variables;
- debug problematic code using strategically placed System.out.println() statements;
- extract values from a UI element; and
- design a set of test cases to help ensure program correctness.
This problem set is due before 5th Period on 2 December 2015. Since many of you will be working in pairs to complete this problem set, make sure you arrange to spend time working together outside of class to meet the due date. And make sure you allocate enough time to complete §![[*]](crossref.png) .
.
It is increasingly important for technology professionals to have good teamwork skills. Not only are many software projects the product of multiple people developing code simultaneously, but the various servers on which an application may be hosted; switches and firewalls carrying traffic to an from an application are used; and database systems managing an application's data all require management by various people. As such, teamwork is very important! And those who develop such skills early are more likely to be more capable team players later.
You are to choose one other person from your period with whom to work on this project. Ideally, this is a person with whom you have not worked with in the past.
3 Warm-Up: Making Combinations
To prepare you to write a program that must try different combinations of values for two variables, you'll first write a program that prints all combinations of first and last names from two ArrayList<String>s.
- Create project ps8 in workspace2. Then create a Java class called AllNames. In it, instantiate and initialize the ArrayList<String>s described below.
| ArrayList<String>'s name |
Contents (elements separated by commas) |
| firstNames |
Carmela, Conrad, Devon, Harry, Jeannie |
| lastNames |
Benson, Dominguez, King, Lam |
- In a main() method, write two nested for() loops. The outer for() loop iterates through values of firstNames, while the inner for() loop iterates through lastNames. Inside the inner for() loop, print one line of text to the console that is the current value from each of firstNames and lastNames, separated by a single space.
Recall that there are two ways to iterate through the elements of an ArrayList. The examples below will iterate through an ArrayList<Integer>, printing each element.
| for-each() version |
for() version |
for ( Integer a : aList ) {
System.out.println( a );
}
|
|
for ( int i = 0 ; i < aList.size() ; i++ ) {
System.out.println( aList.get(i) );
}
|
|
If all went well, there should be a total of 20 unique combinations of first and last name.
#INPUT:signoff-unique-combinations#
Given a quadratic expression in the form 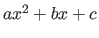 , where
, where
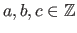 , find integers
, find integers 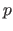 ,
, 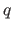 ,
, 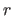 , &
, & 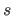 such that
such that
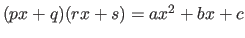 .
. 2
2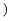 In the case that the quadratic expression isn't factorable using integer values for
In the case that the quadratic expression isn't factorable using integer values for 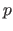 ,
, 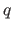 ,
, 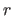 , &
, & 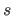 , indicate that the expression is prime.
, indicate that the expression is prime.
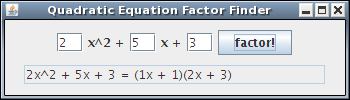
A simple GUI has been built for you according to the MVC [Model-View-Controller] design pattern discussed in class for the Craps application.
- Model: The QuadraticEqn class represents (models) a quadratic equation, with its
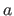 ,
,  , and
, and 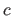 coefficients (as in
coefficients (as in  ). This class is to have one or more methods responsible for finding
). This class is to have one or more methods responsible for finding 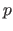 ,
, 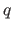 ,
, 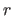 &
& 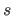 . Any methods and fields added to this class must adhere to safe data access practices, i.e., using private and accessor/mutator methods.
. Any methods and fields added to this class must adhere to safe data access practices, i.e., using private and accessor/mutator methods.
- View: The FactorQuadraticUI class provides a GUI that allows a user to input values for
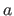 ,
,  , &
, & 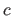 . There is a button that allows the user to request the binomial factors for the given quadratic expression.
. There is a button that allows the user to request the binomial factors for the given quadratic expression.
- Controller: The
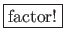 button gives the user control over the application. Clicking the button initiates the method inside QuadraticEqn that finds
button gives the user control over the application. Clicking the button initiates the method inside QuadraticEqn that finds 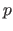 ,
, 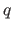 ,
, 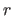 , &
, & 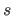 . For simplicity, the controller functionality is actually inside the view class.
. For simplicity, the controller functionality is actually inside the view class.
The entire application is comprised of three classes.
- FactorQuadratic is the driver class. It creates an object of type QuadraticEqn, and passes that object to a new FactorQuadraticUI instance.
- FactorQuadraticUI handles creation of the UI. It also houses the controller functionality, providing the
 button and connecting it to the actionPerformed() method (which triggers the factoring method and updates the UI with the results).
button and connecting it to the actionPerformed() method (which triggers the factoring method and updates the UI with the results).
- QuadraticEqn will be written entirely by you! This class represents a quadratic equation and provides the machinery to factor the quadratic expression,
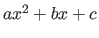 .
.
- Create a new project in workspace2 called PS8FactorQuadratic.
- Download and import FactorQuadratic.java and FactorQuadraticUI.java from
http://feromax.com/apcs/problemsets/PS08/downloads/.
- If you try running the driver, FactorQuadratic, it won't work -- there's no QuadraticEqn class present. Create an empty class (i.e., with no fields or methods) in your project called QuadraticEqn. Now run FactorQuadratic.
Why can FactorQuadratic now successfully create an object of type QuadraticEqn even though that class is void of all methods and fields?
#INPUT:no-args-constructor#
You are to first write a pair of methods -- an accessor and a mutator -- to have a QuadraticEqn object represent a specified equation and then to get the quadratic expression (the non-zero side of the quadratic equation) back out.
- Write a public method called setABC(). It needs to take three int parameters. For example, setABC(1,-2,3) will be used to have QuadraticEqn represent the expression
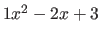 . Add instance variables/fields as needed, being careful to make them private.
. Add instance variables/fields as needed, being careful to make them private.
- Implement a toString() method that returns a String representing the quadratic expression. So if we were to call setABC(1,-2,3), a subsequent call to toString() would return this value: 1x^2 + -2x + 3.
- As a quick test of the two methods you've written, create a main() in QuadraticEqn that creates a few quadratic equations and then prints what toString() returns. Make sure the printed output matches the values you sent to setABC().
#INPUT:test-QuadEqn#
8 Factoring by Hand
Before you're asked to develop the part of this application that actually finds working factors for a given quadratic expression, it might be useful for you (and your partner) to review how you'd identify factors by hand. A pure guess-and-check strategy would involve finding all possible factors for 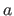 and
and 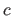 , and then trying different combinations -- including inverting the signs -- until the outer and inner pairs' products sum to the middle term,
, and then trying different combinations -- including inverting the signs -- until the outer and inner pairs' products sum to the middle term, 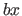 .
.
For the quadratic expressions that follow on the paper form, show all trials (guesses), erasing nothing. You need to develop a sense of how you might have a program try various combinations and how to have your method know when it has found a right answer.
#INPUT:factor-by-hand#
9 Implementing QuadraticEqn, Part II
By now, you should be thinking about how to combine these ideas --
- making combinations (as you did in §3 of this problem set),
- finding the factors of an integer (as we've done in class), and
- taking into account sign changes that are needed when finding correct factorizations (as you should have practiced in the last section)
-- to have a program factor quadratic expressions.
You need to write a public method, getQuadraticFactors(), that returns a String in the form
(px + q)(rx + s),
where 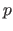 ,
, 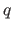 ,
, 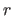 , &
, & 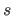 are replaced with correct integer values. If the given quadratic expression is not factorable using integers, return this String: PRIME.
are replaced with correct integer values. If the given quadratic expression is not factorable using integers, return this String: PRIME.
It is recommended that you write a private helper method, called getIntegerFactors(), that getQuadraticFactors() can call upon. If you send getIntegerFactors() an integer, n, it returns an ArrayList<Integer> that contains n's factors. By having a separate method handle this task, we can test the code you write to find factors separately from getQuadraticFactors(), thus making debugging easier.
Here are a few important tips.
- When factoring an integer, it may be easier to factor its absolute value (in the case of a negative integer) and to then use the modulo operator, %.
- When constructing an ArrayList<Integer> object that has all factors of the integer, include both the positive and negative versions of each factor.
- If things don't work as expected, insert System.out.println() statements within your methods, especially within your loops, so you can ``see'' what's really happening.
Once you've implemented at least a stub form of getQuadraticFactors(), uncomment the lines in the actionPerformed() method of the UI class so that the UI is now connected with the methods you're writing.
As a preliminary test, you should feed your GUI the 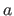 ,
,  , &
, & 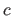 values from the expressions in §
values from the expressions in §![[*]](crossref.png) . Make sure your program's factorizations match what you determined by hand!
. Make sure your program's factorizations match what you determined by hand!
Ordinarily, an application involving a GUI is somehow tested using the GUI, either by hand or using some third-party product that can simulate a user's clicks and typing. In addition, there is usually testing of the underlying components -- classes and methods -- that happens. Part of your grade will be determined by the pass rate your getQuadraticFactors() method gets during an automated test. To make sure your class is prepared, write a tester class to create QuadraticEqn objects, find their factors, and print them. Then, by hand, use FOIL to multiply the binomials together to see if the result matches the quadratic expression you were factoring.
When coming up with test cases, make sure you have quadratic expressions that could be problematic for your program. Mix up the signs, make sure there are multiple factors for 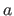 and
and 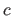 , include expressions you know to be unfactorable, etc.
, include expressions you know to be unfactorable, etc.
How acceptable is your finished product? That will be determined by whether your GUI is working properly and how well your getQuadraticFactors() method performs against predetermined tests.
- GUI Functionality: Demonstrate your (hopefully) finished product.
#INPUT:gui-demo#
- Autotester Results: Download the provided tester class from here -- http://feromax.com/apcs/problemsets/PS08/downloads/tester/ -- and run it against your QuadraticEqn class. Show your teacher the results so that the score may be recorded on your paper form.
#INPUT:autotester-pts#
By now, you should have a solid understanding of how to write a program to factor quadratic expressions. For extra credit and bragging rights, your job is to read over and complete the Javascript included in FactorQuadratic.html available from http://feromax.com/apcs/problemsets/PS08/downloads/bonus/.
- Download FactorQuadratic.html to your Desktop.
- Open the file with your favorite text editor (e.g., gedit).
- Examine the Javascript code between the
 script
script HTML tags (lines 4--88).
HTML tags (lines 4--88).
- Supply the missing code (indicated by the question marks). You'll probably want to search the Web to find Javascript tutorials/references in case you get stuck!
- Load the HTML file in your favorite web browser (e.g., Firefox or Chrome).
- Once done, set var debug = false; to stop the pop-ups that were included to help you troubleshoot your code.
- Attach the HTML file to an email and send to your teacher for extra credit consideration.
#INPUT:bonus#
Footnotes
- ... trinomial1
- Note that
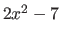 is a quadratic expression but is not a trinomial. And not all trinomials are quadratic, as in
is a quadratic expression but is not a trinomial. And not all trinomials are quadratic, as in
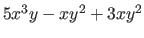 .
.
- ...#tex2html_wrap_inline258#2
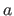 ,
,  ,
,
 means that
means that 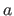 ,
,  , &
, & 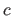 belong to the set of all integers.
belong to the set of all integers.
Michael Ferraro
2015-11-16
![[*]](crossref.png) .
.

![[*]](crossref.png) . Make sure your program's factorizations match what you determined by hand!
. Make sure your program's factorizations match what you determined by hand!
![]() and
and ![]() , include expressions you know to be unfactorable, etc.
, include expressions you know to be unfactorable, etc.